Para este programa, você implementará um programa que executa uma eleição Tideman (ou eleição de pares ranqueados), conforme abaixo.

$ ./tideman Alice Bob Charlie
Number of voters: 5
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob

Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob

Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice

Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice

Rank 1: Charlie
Rank 2: Alice
Rank 3: Bob

Charlie

Introdução ao Exercício

Você já conhece as eleições de pluralidade, que seguem um algoritmo muito simples para determinar o vencedor de uma eleição: cada eleitor recebe um voto, e o candidato com mais votos vence.

Mas o voto de pluralidade tem algumas desvantagens. O que acontece, por exemplo, em uma eleição com três candidatos, e as cédulas abaixo são lançadas?

1tideman

Uma votação de pluralidade aqui declararia um empate entre Alice e Bob, já que cada um tem dois votos. Mas esse é o resultado certo?

Há outro tipo de sistema de votação, conhecido como sistema de votação por classificação/ranqueado. Em um sistema de escolha ranqueada, os eleitores podem votar em mais de um candidato. Em vez de apenas votar na primeira escolha, eles podem classificar os candidatos em ordem de preferência. As cédulas resultantes podem, portanto, parecer como abaixo.

2tideman

Aqui, cada eleitor, além de especificar seu candidato de primeira preferência, também indicou sua segunda e terceira opções. E agora, o que antes era uma eleição empatada agora pode ter um vencedor. A corrida foi originalmente empatada entre Alice e Bob. Mas o eleitor que escolheu Charlie preferiu Alice a Bob, então Alice poderia ser declarada a vencedora.

A votação por escolha ranqueada/classificada também pode resolver outra desvantagem potencial da votação por pluralidade. Confira as votações a seguir.

3tideman

Quem deve ganhar esta eleição? Em uma votação de pluralidade em que cada eleitor escolhe apenas sua primeira preferência, Charlie vence esta eleição com quatro votos em comparação com apenas três para Bob e dois para Alice. (Observe que, se você estiver familiarizado com o sistema de votação de segundo turno instantâneo, Charlie também vence aqui nesse sistema). Alice, no entanto, poderia razoavelmente argumentar que ela deveria ser a vencedora da eleição em vez de Charlie: afinal, dos nove eleitores, a maioria (cinco deles) preferia Alice a Charlie, então a maioria das pessoas ficaria mais feliz com Alice. como o vencedor em vez de Charlie.

Alice é, nesta eleição, a chamada “vencedora de Condorcet” da eleição: aquela que teria vencido qualquer confronto direto contra outro candidato. Se a eleição tivesse sido apenas Alice e Bob, ou apenas Alice e Charlie, Alice teria vencido.

O vencedor de Condorcet, quando existe, é o candidato que venceria cada um dos outros candidatos numa eleição separada só com os dois. Nos exemplos modernos, os eleitores classificarão os candidatos em ordem de preferência.

O método de votação Tideman (também conhecido como “pares classificados”) é um método de votação de escolha classificada que garante a produção do Condorcet vencedor da eleição, se houver.

De um modo geral, o método Tideman funciona construindo um “gráfico” de candidatos, onde uma seta (ou seja, borda) do candidato A para o candidato B indica que o candidato A vence o candidato B em um confronto direto. O gráfico para a eleição acima, então, ficaria como o abaixo.

4tideman

A seta de Alice para Bob significa que mais eleitores preferem Alice a Bob (5 preferem Alice, 4 preferem Bob). Da mesma forma, as outras setas significam que mais eleitores preferem Alice a Charlie e mais eleitores preferem Charlie a Bob.

Olhando para este gráfico, o método Tideman diz que o vencedor da eleição deve ser a “fonte” do gráfico (ou seja, o candidato que não tem seta apontando para ele). Nesse caso, a fonte é Alice — Alice é a única que não tem nenhuma seta apontando para ela, o que significa que ninguém tem preferência frente a frente com Alice. Alice é assim declarada a vencedora da eleição.

É possível, porém, que quando as flechas forem sorteadas, não haja um vencedor Condorcet. Considere as cédulas abaixo.

5tideman

Entre Alice e Bob, Alice é preferida a Bob por uma margem de 7-2. Entre Bob e Charlie, Bob é preferido a Charlie por uma margem de 5-4. Mas entre Charlie e Alice, Charlie é preferido sobre Alice por uma margem de 6-3. Se desenharmos o gráfico, não há fonte! Temos um ciclo de candidatos, onde Alice vence Bob que vence Charlie que vence Alice (muito parecido com um jogo de pedra-papel-tesoura). Nesse caso, parece que não há como escolher um vencedor.

Para lidar com isso, o algoritmo Tideman deve ter cuidado para evitar a criação de ciclos no gráfico candidato. Como ele faz isso? O algoritmo bloqueia as arestas mais fortes primeiro, já que essas são indiscutivelmente as mais significativas. Em particular, o algoritmo Tideman especifica que as arestas de cada “duelo” devem ser “travadas” no gráfico uma de cada vez, com base na “força” da vitória (quanto mais pessoas preferirem um candidato ao invés de seu oponente, mais forte será a vitória). . Desde que a aresta possa ser bloqueada no gráfico sem criar um ciclo, a aresta é adicionada; caso contrário, a aresta é ignorada.

Como isso funcionaria no caso dos votos acima? Bem, a maior margem de vitória para um par é Alice vencendo Bob, já que 7 eleitores preferem Alice a Bob (nenhum outro confronto direto tem um vencedor preferido por mais de 7 eleitores). Portanto, a seta de Alice-Bob é bloqueada no gráfico primeiro. A próxima maior margem de vitória é a vitória de Charlie por 6-3 sobre Alice, de modo que a flecha é a próxima.

A seguir, a vitória de Bob por 5 a 4 sobre Charlie. Mas observe: se fôssemos adicionar uma flecha de Bob para Charlie agora, criaríamos um ciclo! Como o gráfico não pode permitir ciclos, devemos pular essa aresta e não adicioná-la ao gráfico. Se houvesse mais setas a serem consideradas, olharíamos para as próximas, mas essa era a última seta, então o gráfico está completo.

Este processo passo a passo é mostrado abaixo, com o gráfico final à direita.

6tideman

Com base no gráfico resultante, Charlie é a fonte (não há seta apontando para Charlie), então Charlie é declarado o vencedor desta eleição.

Em termos mais formais, o método de votação do Tideman consiste em três partes:

Contagem/Tally : Uma vez que todos os eleitores tenham indicado todas as suas preferências, determine, para cada par de candidatos, quem é o candidato preferido e por qual margem eles são os preferidos.
Classificação/Ordenação/Sort : Classifica os pares de candidatos em ordem decrescente de força de vitória, onde força de vitória é definida como o número de eleitores que preferem o candidato preferido.
Decisão/Lock : Começando com o par mais forte, percorra os pares de candidatos em ordem e “trave” cada par no gráfico candidato, desde que o travamento desse par não crie um ciclo no gráfico.

Assim que o gráfico estiver completo, a fonte do gráfico (aquele sem arestas apontando para ele) é o vencedor!

Começando

Abra o VS Code

1 - Entre no Terminal do VsCode: Ctrl+'

2 - Entrar nessa pasta: cd pset3
OBS: Caso a pasta possua espaço, por exemplo: Semana 3
Será necessário colocar aspas para entrar na pasta: cd 'Semana 3'

3 - No terminal digite o comando: wget https://cdn.cs50.net/2022/fall/psets/3/tideman.zip
seguido de ENTER para baixar o arquivo zipado tideman.zip que contem a pasta tideman com seus arquivos.

4 - Execute o unzip: unzip tideman.zip para extrair a pasta tideman dentro da pasta pset3.

5 - Você não precisa mais do arquivo ZIP, então você pode executar o comando para excluir: rm tideman.zip

6 - Agora entre na pasta: cd tideman

7 - Se tudo foi bem sucedido, você deve executar o comando ls que listará os arquivos dentro dessa pasta, nesse caso deverá ter o arquivo tideman.c
A execução code tideman.c deve abrir o arquivo onde você digitará seu código para este conjunto de problemas. Se não, refaça seus passos e veja se consegue determinar onde errou!

8 - Leia as instruções logo abaixo;

9 - Teste seu código: check50 cs50/problems/2023/x/tideman;

10 - Avalie o estilo do seu código: style50 tideman.c;

11 - Envie seu código: submit50 cs50/problems/2023/x/tideman depois digite: yes

Ver o progresso no Curso

COMPREENSÃO

Vamos dar uma olhada tideman.c.

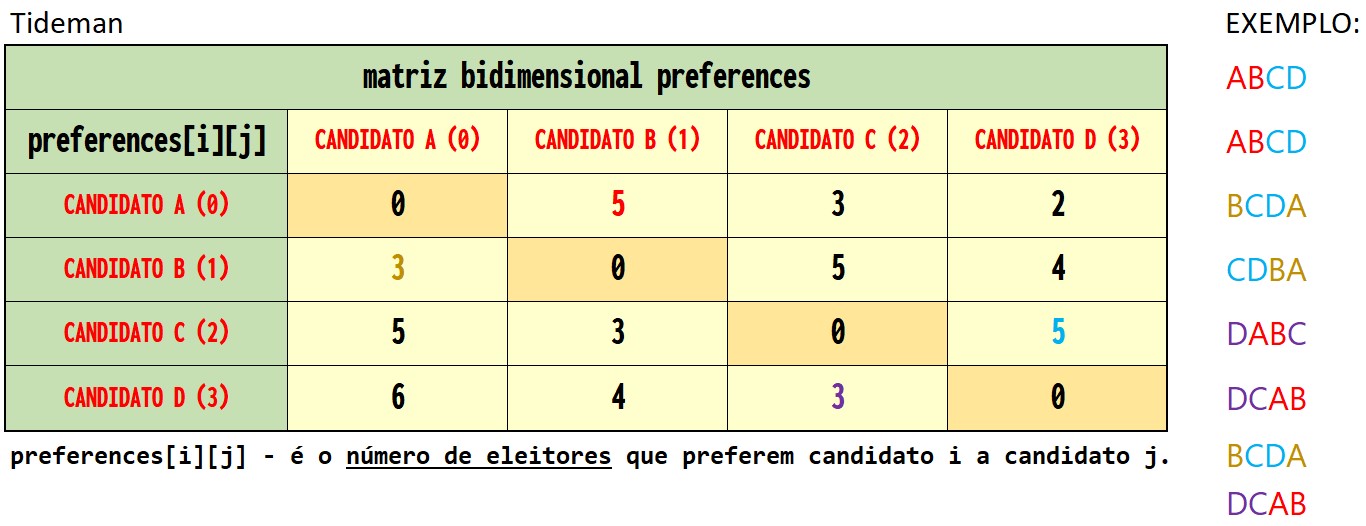
Primeiro, observe a matriz bidimensional preferences. O inteiro preferences[i][j] representará o número de eleitores que preferem candidato i a candidato j.

int preferences[MAX][MAX];

O arquivo também define outro array bidimensional, chamado locked, que representará o grafo candidato. locked é um array booleano, portanto locked[i][j] sendo true representa a existência de uma borda apontando de candidato i a candidato j; false significa que não há borda. (Se curioso, essa representação de um grafo é conhecida como “matriz de adjacência”).

A matriz de adjacências de um grafo é uma matriz booleana com colunas e linhas indexadas pelos vértices.

// locked[i][j] 
// true: significa que existe uma ligação de i apontando para j
// false: significa que não existe borda de ligação
bool locked[MAX][MAX];

O próximo é struct chamado pair, usado para representar um par de candidatos: cada par inclui o índice de candidato vencedor winner e do candidato perdedor loser.

// Cada par tem um vencedor (winner), perdedor (loser)
typedef struct
{
    int winner;
    int loser;
}
pair;

Os próprios candidatos são armazenados no array candidates, que é um array de strings representando os nomes de cada um dos candidatos. Há também uma matriz de pairs, que representará todos os pares de candidatos (para os quais um é preferido em detrimento do outro) na eleição.

// Matriz de candidatos
string candidates[MAX];
pair pairs[MAX * (MAX - 1) / 2];

O programa também possui duas variáveis globais: pair_count e candidate_count, representando o número de pares e número de candidatos nas matrizes pairs e candidates, respectivamente.

// Variáveis globais
int pair_count;
int candidate_count;

Agora em main. Observe que depois de determinar o número de candidatos, o programa percorre o locked gráfico e inicialmente define todos os valores como false, o que significa que nosso gráfico inicial não terá arestas.

    for (int i = 0; i < candidate_count; i++)
    {
        for (int j = 0; j < candidate_count; j++)
        {
            locked[i][j] = false;
        }
    }

Em seguida, o programa percorre todos os votantes e coleta suas preferências em um array chamado ranks(por meio de uma chamada para vote), onde ranks[i] é o índice do candidato que é a i ésima preferência do eleitor. Essas classificações são passadas para a record_preference função, cujo trabalho é obter essas classificações e atualizar a preferences variável global.

    // Consulta de votos
    for (int i = 0; i < voter_count; i++)
    {
      // ranks[i] é a ith(i-ésima) preferência do eleitor
      int ranks[candidate_count];

      // Consulta para cada rank
      for (int j = 0; j < candidate_count; j++) {
        string name = get_string("Rank %i: ", j + 1);

        if (!vote(j, name, ranks)) {
          printf("Invalid vote.\n");
          return 3;
        }
        }

        record_preferences(ranks);

        printf("\n");
    }

Assim que todos os votos forem recebidos, os pares de candidatos são adicionados à pairs matriz por meio de uma chamada para add_pairs, classificados por meio de uma chamada para sort_pairs e bloqueados no gráfico por meio de uma chamada para lock_pairs. Por fim, print_winner é chamado a imprimir o nome do vencedor da eleição!

    add_pairs();
    sort_pairs();
    lock_pairs();
    print_winner();

Mais abaixo no arquivo, você verá que as funções vote, record_preference, add_pairs, sort_pairs, lock_pairs e print_winner são deixadas em branco. Isso é com você!

// Atualizar ranks com novo voto
bool vote(int rank, string name, int ranks[])
{
    // TODO
    return false;
}

// Atualize as preferências dadas as classificações de um eleitor
void record_preferences(int ranks[])
{
    // TODO
    return;
}

// Pares de registro de candidatos onde um é preferido sobre o outro
void add_pairs(void)
{
    // TODO
    return;
}

// Ordene os pares em ordem decrescente de força de vitória
void sort_pairs(void)
{
    // TODO
    return;
}

// Trave os pares no gráfico 'candidato' em ordem, sem criar ciclos
void lock_pairs(void)
{
    // TODO
    return;
}

// Imprima o vencedor da eleição
void print_winner(void)
{
    // TODO
    return;
}

ESPECIFICAÇÃO

Conclua a implementação de tideman.c de modo que simule uma eleição do Tideman.

Conclua a função vote.
- A função recebe os argumentos rank, name e ranks. Se name for uma correspondência para o nome de um candidato válido, você deve atualizar a ranks matriz para indicar que o eleitor tem o candidato como sua rank preferência (onde 0 é a primeira preferência, 1 é a segunda preferência, etc.)
- Lembre-se de que ranks[i] aqui representa a ipreferência do usuário.
- A função deve retornar true se a classificação foi registrada com sucesso, e false caso contrário (se, por exemplo, name não for o nome de um dos candidatos).
- Você pode presumir que não haverá dois candidatos com o mesmo nome.
Conclua a função record_preferences.
- A função é chamada uma vez para cada eleitor, e recebe como argumento o ranks array, (lembre-se que ranks[i] é a i ésima preferência do eleitor, onde ranks[0] é a primeira preferência).
- A função deve atualizar a preferencesmatriz global para adicionar as preferências do eleitor atual. Lembre-se que preferences[i][j] deve representar o número de eleitores que preferem candidato i a candidato j.
- Você pode supor que cada eleitor classificará cada um dos candidatos.
Conclua a função add_pairs.
- A função deve adicionar todos os pares de candidatos em que um candidato é o preferido para o pairs array. Um par de candidatos empatados (um não é preferido sobre o outro) não deve ser adicionado à matriz.
- A função deve atualizar a variável global pair_count para ser o número de pares de candidatos. (Os pares devem, portanto, ser todos armazenados entre pairs[0] e pairs[pair_count - 1], inclusive).
Conclua a função sort_pairs.
- A função deve classificar a pairs matriz em ordem decrescente de força de vitória, onde força de vitória é definida como o número de eleitores que preferem o candidato preferido. Se vários pares tiverem a mesma força de vitória, você pode presumir que a ordem não importa.
Conclua a função lock_pairs.
- A função deve criar o locked gráfico, adicionando todas as arestas em ordem decrescente de força de vitória, desde que a aresta não crie um ciclo.
Conclua a função print_winner.
- A função deve imprimir o nome do candidato que é a fonte do gráfico. Você pode assumir que não haverá mais de uma fonte.

Você não deve modificar nada tideman.c além das implementações das funções vote, record_preferences, add_pairs, sort_pairs, lock_pairs e print_winner(e a inclusão de arquivos de cabeçalho adicionais, se desejar). Você tem permissão para adicionar funções adicionais a tideman.c, desde que não altere as declarações de nenhuma das funções existentes.

PASSO A PASSO

Este vídeo irá te ajudar a entender o problema ;)
Atenção: para adicionar legendas ao vídeo clique no botão CC localizado no Player e selecione a opção “Português (Brasil)”.
Uma excelente aula para você!

CC50: PSet 3 - Tideman

Uso

Seu programa deve se comportar conforme o exemplo abaixo:

./tideman Alice Bob Charlie
Number of voters: 5
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob

Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob

Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice

Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice

Rank 1: Charlie
Rank 2: Alice
Rank 3: Bob

Charlie

Como testar o seu código?

Certifique-se de testar seu código para ter certeza de que ele lida com…

Uma eleição com qualquer número de candidatos (até o MAX de 9)
Votar em um candidato pelo nome
Votos inválidos para candidatos que não constam na cédula
Imprimindo o vencedor da eleição

Voltar ao README

Voltar ao Índice da Semana 3

cs50-cc50-harvard

Exercício 3 - Tideman