Lâmpadas não estão quebradas

Na palestra, você deve ter notado o que parecia ser um “bug” na frente do palco, em que algumas das lâmpadas parecem estar sempre apagadas:

Cada sequência de lâmpadas, no entanto, codifica uma mensagem em binário, a linguagem que os computadores “falam”.

Vamos escrever um programa para fazer suas próprias mensagens secretas, talvez até possamos colocá-las no palco!

Começando

Abra o VS Code

1 - Entre no Terminal do VsCode: Ctrl+'

2 - Entrar nessa pasta: cd pset2
OBS: Caso a pasta possua espaço, por exemplo: Semana 2
Será necessário colocar aspas para entrar na pasta: cd 'Semana 2'

3 - No terminal digite o comando: wget https://cdn.cs50.net/2022/fall/psets/2/bulbs.zip
seguido de ENTER para baixar o zip bulbs.zip que contem a pasta bulbs com o arquivo em C.

4 - Execute o unzip: unzip bulbs.zip para extrair a pasta bulbs dentro da pasta pset2.

5 - Você não precisa mais do arquivo ZIP, então você pode executar o comando para excluir: rm bulbs.zip

6 - Agora entre na pasta: cd bulbs

7 - Se tudo foi bem sucedido, você deve executar o comando ls que listará os arquivos dentro dessa pasta, nesse caso deverá ter o arquivo bulbs.c
A execução code bulbs.c deve abrir o arquivo onde você digitará seu código para este conjunto de problemas. Se não, refaça seus passos e veja se consegue determinar onde errou!

8 - No arquivo bulbs.c faça o exercício proposto;

9 - Teste seu código: check50 cs50/problems/2023/x/bulbs;

10 - Avalie o estilo do seu código: style50 bulbs.c;

11 - Envie seu código: submit50 cs50/problems/2023/x/bulbs depois digite: yes

Detalhes da Implementação

Para escrever nosso programa, primeiro precisamos pensar em bases.

O básico

A base mais simples é a base-1, ou unária; para escrever um número, N , na base-1, simplesmente escreveríamos N s consecutivos 1. Portanto, o número 4 na base 1 seria escrito como 1111, e o número 12 como 111111111111. Pense nisso como contar nos dedos ou marcar uma pontuação com marcas em um quadro.

Você pode ver porque a base-1 não é muito usada hoje em dia. (Os números ficam bastante longos!) Em vez disso, uma convenção comum é a base 10, ou decimal. Na base 10, cada dígito é multiplicado por alguma potência de 10, para representar números maiores. Por exemplo, 123 é curto para 123 = 1.10² + 2.10¹ + 3.10°.

Mudar de base é tão simples como mudar o 10
acima para um número diferente. Por exemplo, se você escreveu 123 na base 4, o número que você realmente escreveria é 123 = 1.4² + 2.4¹ + 3.4°, que é igual ao número decimal 27.

Os computadores, no entanto, usam base-2 ou binário. Em binário, escrever 123 seria um erro, já que os números binários só podem ter 0s e 1s. Mas o processo de descobrir exatamente qual número decimal um número binário representa é exatamente o mesmo. Por exemplo, o número 10101 na base-2 representa 1.2⁴ + 0.2³ + 1.2² + 0.2¹ + 1.2°, que é igual ao número decimal 21.

Sistema Unário B = 1 (1);
Sistema Binário B = 2 (0 e 1);
Sistema Decimal B = 10 (0 a 9);
Sistema Hexadecimal B = 16 (0 a 9, A a F);
Sistema Octal B = 8 (0 a 8)

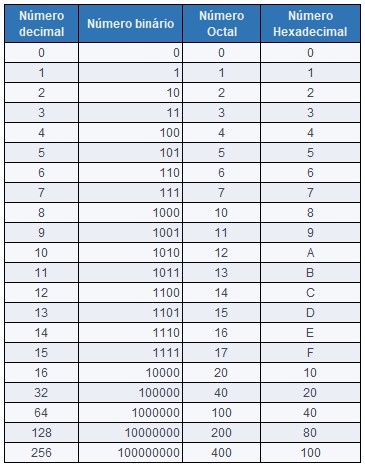
Codificando uma mensagem

As lâmpadas só podem estar acesas ou apagadas. Em outras palavras, as lâmpadas representam dois estados possíveis; ou a lâmpada está acesa ou apagada, assim como os números binários são 1 ou 0. Teremos que encontrar uma maneira de codificar o texto como uma sequência de números binários.

Vamos escrever um programa chamado bulbs que pega uma mensagem e a converte em um conjunto de lâmpadas que podemos mostrar a um público desavisado. Faremos isso em duas etapas:

O primeiro passo consiste em transformar o texto em números decimais. Digamos que queremos codificar a mensagem HI!. Felizmente, já temos uma convenção sobre como fazer isso, ASCII. Observe que H é representado pelo número decimal 72, I é representado por 73 e ! é representado por 33.

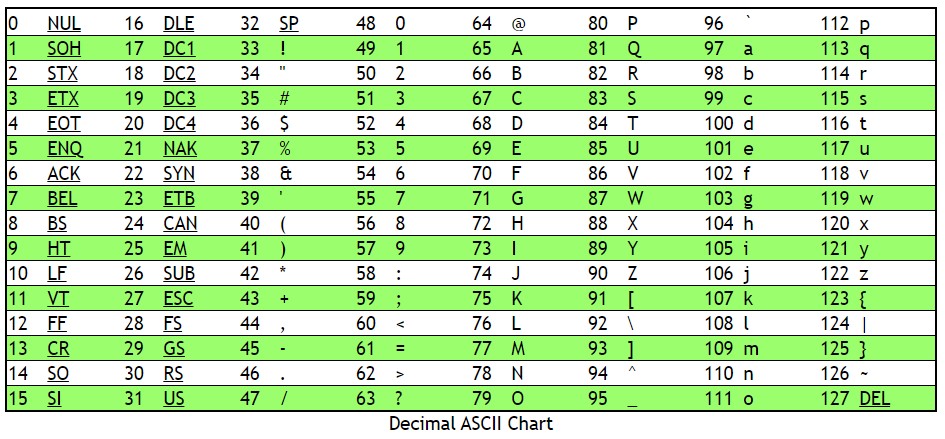
A próxima etapa envolve pegar nossos números decimais (como 72, 73 e 33) e convertê-los em números binários equivalentes, que usam apenas 0s e 1s. Para ter um número consistente de bits em cada um de nossos números binários, suponha que cada decimal seja representado com 8 bits. 72 é 01001000, 73 é 01001001 e 33 é 00100001.

Por fim, interpretaremos esses números binários como instruções para as lâmpadas no palco; 0 está desligado, 1 está ligado. (Você descobrirá que bulbs.c inclui uma print_bulb função que foi implementada para você, que recebe um 0ou 1 e emite emojis que representam lâmpadas.)

Aqui está um exemplo de como o programa concluído pode funcionar. Ao contrário do palco Sanders (Theatre, na Universidade Harvard), imprimiremos um byte por linha para maior clareza.

# ./bulbs
Message: HI!
⚫🟡⚫⚫🟡⚫⚫⚫
⚫🟡⚫⚫🟡⚫⚫🟡
⚫⚫🟡⚫⚫⚫⚫🟡

Para verificar nosso trabalho, podemos ler uma lâmpada acesa (🟡) como 1 e uma lâmpada apagada (⚫) como 0. Então HI! se tornou

01001000
01001001
00100001

que é precisamente o que esperaríamos.

Outro exemplo:

# ./bulbs
Message: HI MOM
⚫🟡⚫⚫🟡⚫⚫⚫
⚫🟡⚫⚫🟡⚫⚫🟡
⚫⚫🟡⚫⚫⚫⚫⚫
⚫🟡⚫⚫🟡🟡⚫🟡
⚫🟡⚫⚫🟡🟡🟡🟡
⚫🟡⚫⚫🟡🟡⚫🟡

Observe que todos os caracteres estão incluídos nas instruções da lâmpada, incluindo caracteres não alfabéticos como espaços = decimal 32 (00100000).

Especificação

Projete e implemente um programa, bulbs, que converta texto em instruções para a faixa de lâmpadas no palco do CS50 da seguinte forma:

Implemente seu programa em um arquivo chamado bulbs.c.
Seu programa deve primeiro solicitar uma mensagem ao usuário usando get_string.
Seu programa deve então converter o dado string em uma série de números binários de 8 bits, um para cada caractere da string.
Você pode usar a print_bulb função fornecida para imprimir uma série de 0s e 1s como uma série de emojis amarelos e pretos, que representam lâmpadas acesas e apagadas.
Cada “byte” de 8 símbolos deve ser impresso em sua própria linha quando gerado; deve haver um \n após o último “byte” de 8 símbolos também.

Dicas de Decimal para Binário

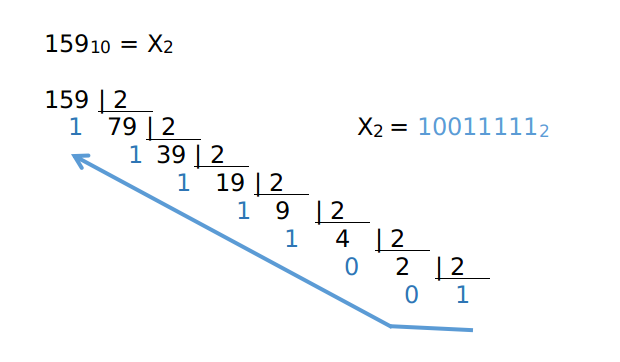
Vamos ver um exemplo com o número 4. Como você converteria 4 em binário? Comece considerando o bit mais à direita, aquele que — se ativado — adiciona 1 ao número que estamos representando. Você precisa deste bit para estar ligado? Divida 4 por 2 para descobrir:

4/2 = 2

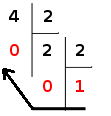
2 divide igualmente em 4, o que nos diz que não há resto de 1 para se preocupar. Podemos deixar esse bit mais à direita com segurança, então:

E quanto ao bit anterior, agora, aquele logo à esquerda desse bit que descobrimos? Para verificar, vamos seguir um processo semelhante, mas continuar de onde paramos. No passo anterior, dividimos 4 por 2 e obtivemos 2. Agora, 2 divide igualmente em 2? Sim, então não há resto de 2 para se preocupar:

Vamos continuar ainda mais. Depois de dividir 2 por 2, ficamos com 1. Dividir 1 por 2 deixa um resto de 1. Isso significa que precisaremos ativar este bit:

E agora que dividimos nosso número até 0, não precisamos de mais bits para representá-lo. Observe que descobrimos que os bits representam 4 na ordem oposta em que precisamos imprimi-los: provavelmente precisaremos de uma estrutura que nos permita armazenar esses bits, para que possamos imprimi-los adiante mais tarde.

E, claro, em seu código real, você estará trabalhando com chars de 8 bits, então você vai querer preceder qualquer 0 necessário.

Ao verificar os restos, o operador módulo (%) pode ser útil! 4 % 2, por exemplo, retorna 0, o que significa que 4 se divide em 2 com um resto de 0.

Voltar ao README

Voltar ao Índice da Semana 2

cs50-cc50-harvard

Exercício 4 - Bulbs (Lâmpadas)